Fatoração e produtos notáveis

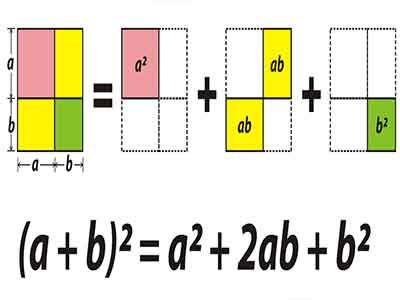
PRODUTOS NOTÁUEIS E FATORAÇÃO

O conhecimento que temos hoje sobre a Matemática do antigo Egito tem como base dois grandes documentos, cujos textos estão escritos em papiros. O mais antigo é conhecido por Papiro Rhind, o outro é o Papiro de Moscou. Eles são compostos de problemas e resoluções, razão pela qual se supõe que tenham sido destinados ao ensino dos funcionários do Estado e dos escribas dos faraós.

Veja o Slide logo abaixo e depois acompanhe a o resumo

0 Papiro Rhind é considerado o mais precioso documento relativo aos conhecimentos matemáticos dos egípcios e data, aproximadamente, de 1650 a.C. Em forma de manual prático, contém uma coleção de 85 problemas de Aritmética e Geometria, em sua maioria envolvendo assuntos do cotidiano, como o preço do pão e a armazenagem de grãos de trigo. Seu nome se deve a um antiquário escocês,

i Alexander Henry Rhind, que o comprou em 1808, no Egito. Após sua – morte, cinco anos depois, o papiro foi adquirido pelo British Museum de Londres, onde se encontra atualmente.

O Papiro Rhind é também denominado Papiro Ahmes em homenagem ao escriba egípcio que o copiou, em escrita hierática (sagrada), de um manuscrito mais antigo, de cerca de duzentos anos antes.

Os problemas apresentados nos papiros eram resolvidos por processos aritméticos comuns para os egípcios. No Papiro Rhind, Ahmes utilizava um processo conhecido como método da falsa posição para resolver problemas que envolviam equações lineares com uma incógnita {x + ax = b, por exemplo). Nesse processo, um valor específico, provavelmente falso, é assumido para x, e as operações indicadas à esquerda da igualdade são efetuadas para esse valor; o resultado é então comparado com o resultado que se pretende e, usando-se proporções, chega-se à resposta correta. Ahmes também utilizava, às vezes, outro método chamado método da fatoração, que consistia em colocar o aha (a incógnita) em evidência no lado esquerdo da igualdade e dividir ambos os membros da equação por seu coeficiente. Certamente esse último processo é familiar a você, já que corresponde a um dos casos de fatoração estudados anteriormente.

Os conceitos e procedimentos algébricos serão aqui revistos e aprofundados a fim de prepará-lo para novas aplicações.

1.  Produtos notáveis

Alguns produtos que envolvem expressões algébricas apresentam um padrão, uma regularidade em seus resultados. Por isso são conhecidos como produtos notáveis. Conhecendo-os, podemos economizar muitos cálculos.

Vamos estudar os produtos notáveis conhecidos por quadrado da soma, quadrado da diferença, produto da soma pela diferença, cubo da soma e cubo da diferença.

Quadrado de uma soma indicada: (a + b)² ou (a + b)(a + b)

(a + b)² = (a + b)(a + b) = a- a + a- b + b- a + b- b = a² + 2ab + b²

Assim:

(a + b)² = a² + 2ab + b² Geometricamente, é o mesmo que calcular a área da região quadrada de lado (a + b).

Ao dividir o lado do quadrado em duas partes de medidas a e b, a região quadrada fica dividida em quatro partes: duas retangulares de área ab cada uma, uma quadrada de área a² e outra quadrada de área b².

Veja alguns exemplos:

• (3x + 5)²= 9x²+ 30x + 25    •    (y    +    6)²    =    y² + 12y + 36

(3x)²    2    •    (3x)    •    5    5²

Quadrado de uma diferença indicada: (a – b)² ou (a – b)(a – b)

(a – b)² = (a – b)(a -b) = a- a- a- b- b- a + b- b = a²– 2ab + b²

Assim:

(a – b)² = a² – 2ab + b²

Geometricamente, equivale a calcular a área da região quadrada de lado (a – b).

Veja alguns exemplos:

(x – 4)² = x² – 8x + 16

Produto de uma soma indicada por uma diferença indicada: (a + b)(a-b)

(a + b)(a – b) = a² – ab + ba – b² = a² – ab – ab – b² = a² – b² 4 4

Assim:

(a + b)(a – b) = a² – b²

Geometricamente, equivale a calcular a área da região retangular de lados (a + b) e (a – b).

Veja alguns exemplos:

(x² + x)(x² — x) = x⁴ – X²

(5x + y)(5x – y) = 25x² – y²

(3x + 7)(3x – 7) = 9x² – 49

Cubo de uma soma indicada: (a + b)³

(a + b)³ = (a + b)(a + b)² = (a + b) • (a² + 2ab + b²) = a³ + 2a²b + ab² + ba² + 2ab² + b³ = a³ + 3a²b + 3ab² + b³

Assim:

(a + b)³ = a³ + 3a²b 4- 3ab² + b³ Capitulo 1 | Revisão: produtos notáveis e fatoração

Geometricamente, (a + b)³ indica o volume de um cubo com arestas que medem a + b. Esse cubo pode ser dividido em: um cubo de arestas a (a³), três paralelepípedos de arestas a, a e b (3a²b), três paralelepípedos de arestas a, b e b (3ab²) e um cubo de arestas b (b³).

•    (x + 3)³= x³+ 3    • x²    • 3 + 3 • x • 3² + 3³ = x³ + 9x² + 27x + 27
•    (2a + b)³= (2a)³   + 3    • (2a)² •b + 3-2a-b² + b³ = 8a³ + 12a²b + 6ab²    +    b³

Cubo de uma diferença indicada: (a – b)³

(a – b)³ = (a – b) • (a – b)² = (a – b)(a² – 2ab + b²) = a³ – 2a²b + ab² – a²b + 2ab² – b³ = a³ – 3a²b + 3ab² – b³ Assim:

(a – b)³ = a³ – 3a²b + 3ab² – b³

Veja alguns exemplos:

•    (x –4)³= x³ – 3    • x²    • 4 + 3 • x • 4² – 4³ = x³ – 12x² + 48x – 64
•    (3x – y)³= (3x)³   – 3    • (3x)² • y + 3 • (3x) • y² – y³ = 27x³ – 27x²y    + 9xy² – y³

2. Fatoração de expressões algébricas

Fatorar uma expressão algébrica é transformá-la em um produto.

Existem vários casos de fatoração que devem ser utilizados de acordo com as características da expressão algébrica a ser fatorada.

I⁹ caso de fatoração: colocação de um termo em evidência

Vamos fatorar 3a² + 3ab.

3a é o fator comum às duas parcelas de 3a² + 3ab. Assim:

3a² + 3ab = 3a(a + b)

forma fatorada

Em 4x + 6, o 2 é o fator comum das duas parcelas. Então, 4x + 6 = 2(2x + 3).

2⁹ caso de fatoração: agrupamento

Analise com atenção a expressão algébrica de quatro termos ax + 2a + 5x + 10. Não existe um fator comum aos quatro termos. Mas, agrupando-os de forma conveniente, podemos fazer a sua fatoração aplicando duas vezes o 1⁹ caso de fatoração. Veja:

ax + 2a + 5x + 10

a(x + 2) + 5(x + 2)

(x + 2) • (a + 5)

Veja outros exemplos: ab + a – bx – x

a(b + 1) – x(b + 1)

• a²– 5a + a – 5

a(a — 5) + 1(a – 5)

x³ – 2x² – x + x²y – 2xy + y

x(x² – 2x -I-1) + y(x² – 2x + 1)

(x² – 2x + 1)(x + y)

(b + 1 )(a – x)

(a-5)(a + 1)

3⁹ caso de fatoração: trinômio quadrado perfeito

No estudo dos produtos notáveis você viu que o quadrado da soma e o quadrado da diferença de dois termos nos dão trinômios como resultados. Por exemplo:

•    (x + 5)²= x²+IOx + 25    •    (a – 7)² = a² — 14a + 49
•    (3x+ 10)²= 9x²+ 60x+ 100    •    (4x – 9y)² = 16x² – 72xy – Sly²

Cada um dos trinômios obtidos é conhecido por trinômio quadrado perfeito. O caminho inverso do que aparece acima é a fatoração do trinômio. Veja:

•    x²+ 1 Ox + 25 = (x + 5)²   •    16x²-72xy + 81y² = (4x-9y)²

quadrado quadrado    (4x)²    0y)²

de x        de    5    -2-(4x)-(9y)

o dobro do produto de x e 5

Exemplo:

^|f (Ibmec-SP) No bolso de uma pessoa havia X cédulas de Y reais e Y cédulas de X reais. Se esta pessoa colocar neste bolso mais X cédulas de X reais e Y cédulas de Y reais, então esta pessoa terá no bolso:

tim-tim por tim-tim

1. a) (X + Y)²    c) (X²+ Y²) reais.    e) (X² + Y²)² reais.
2. b) (X – Y)²    d) (X²– Y²) reais.
3.    Lendo e compreendendo
4. a)    O que é dado no problema?

São dadas as quantidades de cédulas de X reais e a quantidade de cédulas de Y reais.

1. b)    O que se pede?

Pede-se que se estabeleça a quantidade de dinheiro que a pessoa tem no bolso.

2.    Planejando a soluçãoComo sabemos a quantidade de cédulas deX e de Y reais que a pessoa tinha no bolso, basta multiplicar a quantidade de cédulas pelo seu valor para ter o total de dinheiro. Depois, somaremos todos esses valores e, se necessário, manipularemos a expressão obtida para chegar à resposta correta.
3.    Executando o que foi planejadoAntes, havia no bolsoX cédulas de Y reais, totalizando X • Y reais; e havia Y cédulas de X reais, totalizando mais X • Y reais.

Assim, inicialmente, ela tinha XY + XY, ou seja, 2XY reais no bolso.

Depois, ela colocou mais X cédulas de X reais, totalizando X • X, ou seja, X² reais; e colocou também Y cédulas de Y reais, totalizando mais Y • Y, ou seja, Y² reais.

Assim, ela terá no bolso X² + 2XY + Y².

4.    Emitindo a resposta

Para chegar à resposta, é necessário fatorar a expressão inicialmente obtida. Devemos perceber então que se trata de um trinômio quadrado perfeito:

X² + 2XY + Y² = (X + Y)² A resposta é o item a.

5.    Ampliando o problema Discussão em equipe

Troque ideias com seus colegas sobre como alterar o enunciado para que o resultado seja o item b das alternativas.

4⁹ caso de fatoração: diferença de dois quadrados

Você já viu que o produto da soma pela diferença dos mesmos termos é um produto notável e que seu resultado é igual à diferença entre o quadrado do 1⁹ termo e o quadrado do 2- termo. Por exemplo:

• (x +8)(x -8) = x² – 64    •    (7x    +    y)(7x    —    y)    =    49x² – y²
• (5x + 9)(5x — 9) = 25x²— 81    •    (10    +    a)(10    –    a)    =    100 – a²

O caminho inverso do que aparece acima é a fatoração da diferença de dois quadrados. Veja:

•    x²— 64 = (x +8)(x — 8)    •    25x²    —    81    =    (5x    +    9)(5x    —    9)    •    100    –    a²    =    (10    +    a)(10    –    a)

quadrado    quadrado    de    8    (5x)²    9²    10²    a²

de x

5⁹ caso de fatoração: soma de dois cubos

Veja o que acontece quando multiplicamos a soma de dois termos por um trinômio formado pelo quadrado do 1⁹ termo, menos o produto do I⁹ pelo 2⁹ e mais o quadrado do 2⁹ termo:

•    (x + y)(x²– xy + y²) = x³– f    y³ = x³ + y³

cubo de x cubo de y

•    (5x + 2)(25x²– 10x + 4) = 125x³– 50x^+    $0^-    + 8 = 125x³ + 8

cubo de 5x    cubo de 2

O caminho inverso do que aparece acima é mais um caso de fatoração (soma de dois cubos). Veja:

•    x³+ y³= (x + y)(x² – xy + y²)    •    125x³ + 8 = (5x + 2)(25x² – 10x + 4)

cubo de x    cubo de y    (Sx)³ 2^a

6– caso de fatoração: diferença de dois cubos

O raciocínio é o mesmo do caso anterior:

•    (x – y)(x²+ xy + y²) = x³+    +    xy²-yx²-xy^r– y³ = x³ – y³

7- caso de fatoração: fatoração de expressões quadráticas

Quando multiplicamos (x + 3) por (x + 2) obtemos x² + 5x + 6, ou seja:

(x + 3)(x + 2) = x² + 5x + 6

O processo inverso, ou seja, partindo de x² + 5x + 6 para chegar a (x + 3)(x + 2), é chamado de fatoração da expressão quadrática x² + 5x + 6.

Veja alguns exemplos de fatoração de expressões quadráticas:

•    x²+6x + 8

Devemos encontrar dois números cujo produto é 8 e cuja soma é 6. Esses números são 4 e 2. Então,

x² + 6x + 8 = (x + 4)(x + 2).

•    x²-6x + 8

Devemos encontrar dois números cujo produto é 8 e cuja soma é -6. Esses números são -2 e -4. Então,

x² – 6x + 8 = (x – 2)(x – 4).

Resolução da equação do 2– grau usando fatoração de expressões quadráticas

Vamos resolver a equação do 2- grau x² + x – 12 = 0.